Is Power Proportional to Resistance or not?

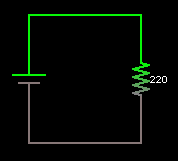
I'm finally home for the summer! Sorry for the absence of posts lately, but there was something that caught my mind the other day. Is power proportional to resistance? Naturally, I started jotting down Ohm's Law. For those of you who don't know, check my last post for a rant about Ohm's Law (TL;DR - V=IR).

To find the power dissipated across a resistor (or any Ohmic load) we present the following scenario (please forgive my handwritten notes in advance). The voltage across the resistor is represented in Volts, which is the energy in Joules per unit charge in Coloumbs. Likewise, the current flowing through the resistor in Amperes (A) is the amount of charge (C) per second (s). If we multiply the voltage and current together, the charges cancel out and we obtain that P = VI. If we substitute Ohm's Law into the previous equation we can rewrite the power formula as (I^2)R or (V^2)/R. 

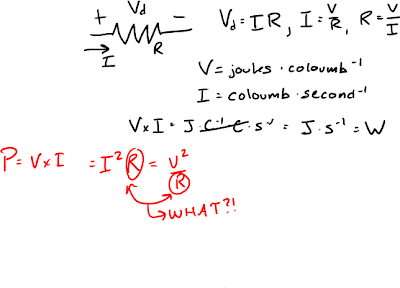Yes, I showed my work...

This presents a predicament to me - is dissipated power proportional to resistance or not? There are three possible scenarios. 

1. The power is proportional to the resistance based on the equation P = (I^2)*R. 
2. The power is inversely proportional the resistance based on the equation P = (V^2)*R.
3. The power is independent of the resistance and is constant for a fixed resistance regardless of voltage and current changes. 

I suppose another scenario is that Georg Ohm was a fraud and one of the fundamental principles of electrical engineering is complete bogus. However, I highly doubt that is the case.

To figure this out, I decided to run a quick program in MATLAB. Here is the source code:

Sorry that it's going off the border; I was going for readability. 

And the results...

I suppose it was redundant to plot the same quantity three times.

So according to this, it is scenario 2. If we substitute I=V/R into P=I^2*R, we get that P = (R*V^2)/R^2. There is a greater power of R in the denominator, and therefore we can say with confidence that the power dissipated across a resistor is inversely proportional to the resistance. 


Thanks for reading!


~Mike

Overteaching Ohm's Law?

Since I took my first Physics class during my junior year of high school, I have been taught Ohm's Law maybe three or four times now: once then, once in PHYS 2306 (Physics for Engineers II), ECE 2004 (Electric Circuit Analysis) and the lab for that class. 


I am not saying that Ohm's Law isn't valuable - rather it's one of the only concepts in circuits that you can teach without using advanced math such as calculus and differential equations (which is most likely why most curricula don't proceed further until college). 


However, it's not as effective to teach Ohm's Law without connecting it to Kirchoff's Voltage Laws (aka Loop Rule). KVL states that all of the rises and drops in voltage must equal zero. So if we have a circuit like the one below (the battery supplies 5 V). 

We can see that all five volts are dissipated across the resistor, so the KVL is satisfied. In my opinion we should teach students that the current going through a resistor is ΔV/R rather than just V/R. That way it will include the voltage drop. 


Now let's put this teaching into practice. For our first assignment in 2074 (circuits lab) we had to construct the following circuit (very easy)

Now that there are two resistors, all five volts aren't being dissipated across one resistor. 
We weren't supposed to know what the last resistor was, and calculate it based on the voltage across that resistor and KVL, even though we could have just used a DMM or just figured it out through the colors.


Using a multimeter, I measured that the voltage drop across the resistor was around 3.24 V and that the current flowing through that resistor was 3.96 mA. We can rearrange the ΔV/R equation from earlier to get that R = ΔV/I. 


R = ΔV/I
R = 3.24 V/ 3.96 mA
R = 818 Ω


The resistor was actually 813 Ω, which is within 5% tolerance and acceptable. The final wiring looked something like this.

So that's it for now - my next post will be on the board above, which we call the ANDY board. 

Hello everyone and welcome to my Electronics Blog! I'll try to update this as often as I can so that you can follow along with what I'm doing. 

For starters, I'm a second semester sophomore Electrical Engineering student at Virginia Tech. I will be discussing the lab portions of two courses - ECE 2074 (Electric Circuits Lab) and ECE 2504 (Intro to Computer Engineering). The former concerns itself with very basic analog components (resistors, capacitors, inductors, etc.) and will be showing you the different circuits I've built for that class and what I've learned from there. 2504 doesn't have as many circuits to build but I'll certainly show you what we do in class.

So whether it's your first time learning about electronics or a grizzled EE veteran refreshing your memory enjoy the blog! For now, I have a test in 2504 tomorrow so I'll post the first bit from 2074 after the test.  I'll also let you know how that goes.

PS, the picture here is outside of Durham and Whittemore Hall, the two main EE buildings here at Virginia Tech, just a few days ago.